第8节 树

在实际生活中，可以用线性结构描述数据元素之间逻辑关系的问题是很广泛的，但也有很多问题不能依靠线性结构来解决，例如家谱、行政组织机构等都是非线性的数据结构。其中树就是一种非线性的数据结构。

一、树的定义

树作为一种非线性的数据结构，是由 $n(n ≥0)$ 个结点组成的有限集合。

1. 如果n为0时，树为空树；
2. 如果 $n>0$ 时，树有一个特定的结点——根结点。

根结点只有直接后继，没有直接前驱。除根结点以外的其他结点划分为 $m(m ≥0)$ 个互不相交的有限集合T0,T1,T2,.,Tm-1，每个集合是一棵树，称为根结点的子树。树的示例如下:

二、树的相关概念

1. 树的度：结点拥有的子树的数量为结点的度，度为0的结点是叶结点，度不为0的结点为分支结点，树的度定义为树的所有结点中度的最大值。

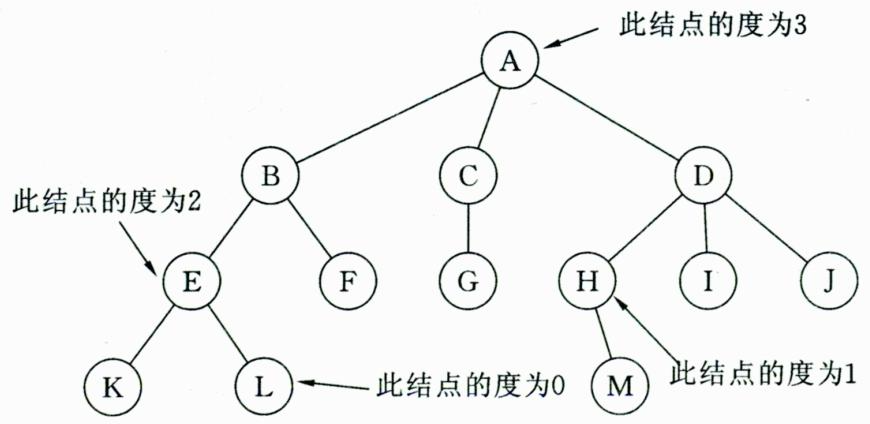
2. 树的前驱和后继：除根结点没有前驱外，其余每个结点都有唯一的一个前驱结点。每个结点可以有0或多个后继结点。结点的直接后继称为结点的孩子，结点的直接前驱称为结点的父亲。结点的孩子的孩子称为结点的孙子，结点称为子孙的祖先。同一个双亲的孩子之间互称兄弟。

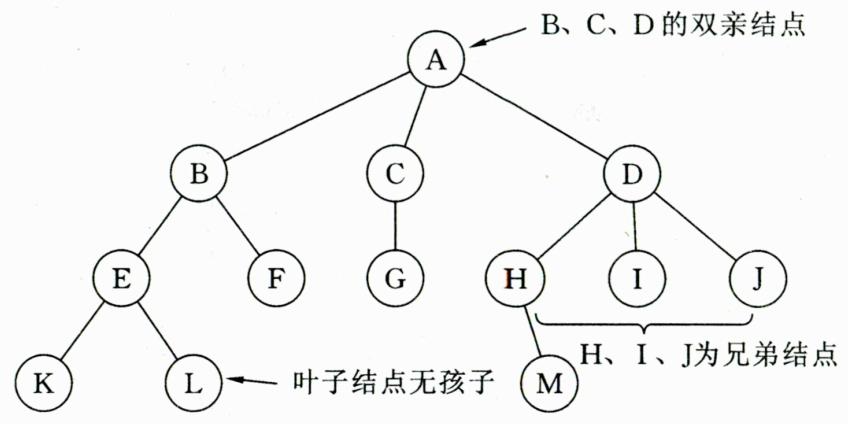
B、C、D的双亲结点是A，H、I、J为兄弟结点，H是叶子结点无孩子。 3. 树中结点的层次：树中根结点为第1层，根结点的孩子为第2层，依次类推。树中结点的最大层次称为树的深度或高度。

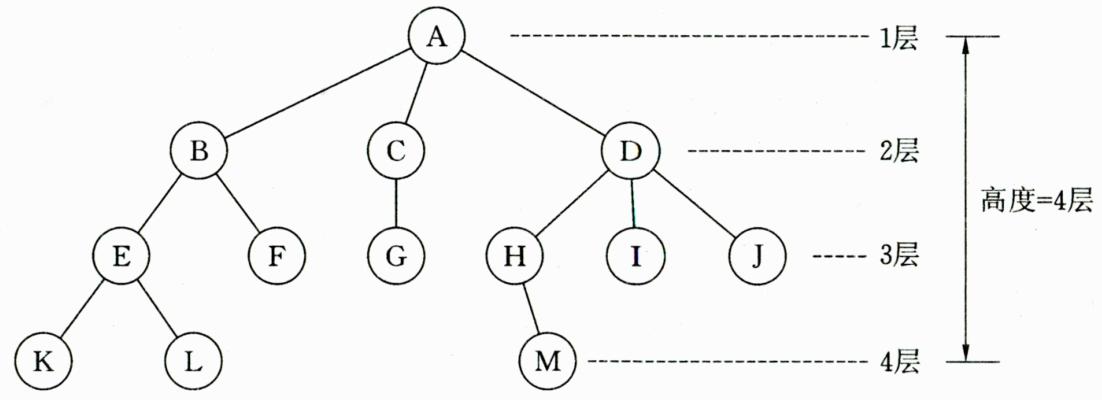
4. 森林：是由 $n(n>=0)$ 棵互不相交的树组成的集合。

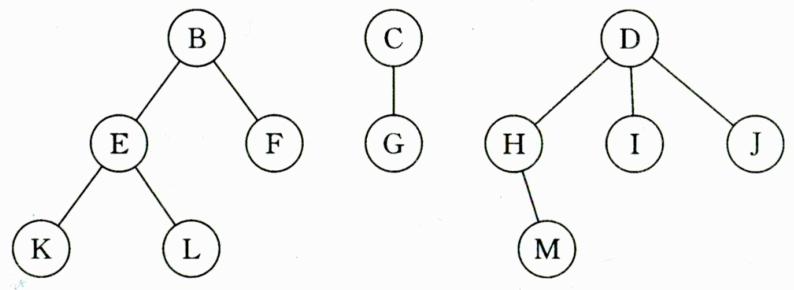
三、树的性质

1. 除根结点没有父结点外，其余结点有且仅有一个父结点。
2. n个结点的树，有且仅有 $n - 1$ 条边。
3. 树中任意两个结点之间有且仅有一条简单路径(指路径上的顶点都不相同的路径，不存在自环和重边)。

四、二叉树

二叉树(binary tree，简写BT)是一种度数为2的树，即二叉树的每个结点最多有两个子结点。每个结点的子结点分别称为左孩子、右孩子，它的两棵子树分别称为左子树、右子树。

1. 二叉树的遍历

所谓的遍历是指按一定的规律和次序访问树中的各个结点，而且每个结点仅被访问一次。遍历一般按照从左到右的顺序，共有4种遍历方法：前序遍历、中序遍历、后序遍历、层次遍历。

• 先序遍历：先访问根结点，再访问左子树，最后访问右子树。
• 后序遍历：先左子树，再右子树，最后根结点。
• 中序遍历：先左子树，再根结点，最后右子树。
• 层次遍历：每一层从左到右访问每一个结点。

例1：求下图所示树的各种遍历结果。

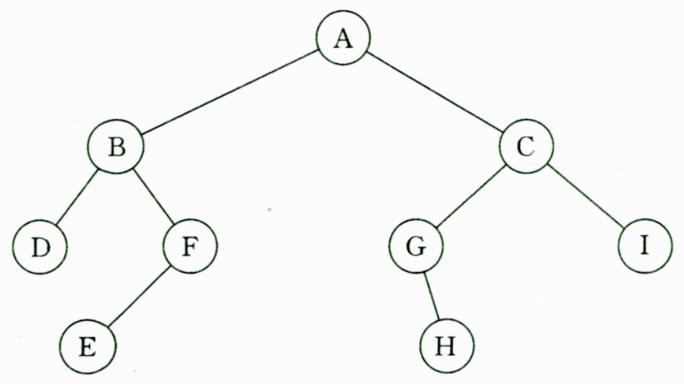
先序遍历结果：ABDFECGHI。
中序遍历结果：DBEFAGHCI。
后序遍历结果：DEFBHGICA。
层次遍历结果：ABCDFGIEH。

例2：关于前面讲的表达式树，我们可以分别用先序、中序、后序的遍历方法得出完全不同的遍历结果，如对于下图遍历结果如下，它们正好对应表达式的3种表示方法。

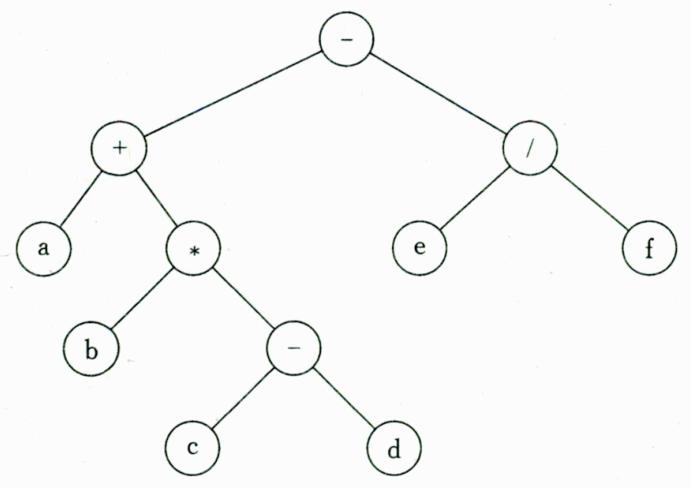
• 前缀表示、波兰式：-+a*b-cd/ef
• 中缀表示：a+b*c-d-e/f
• 后缀表示、逆波兰式：abcd-*+ef/-

结论：已知前序序列和中序序列可以确定出二叉树；已知中序序列和后序序列也可以确定出二叉树；但已知前序序列和后序序列却不可以确定出二叉树。

例3：有二叉树中序序列为ABCEFGHD，后序序列为ABFHGEDC。 请画出此二叉树，并求前序序列。

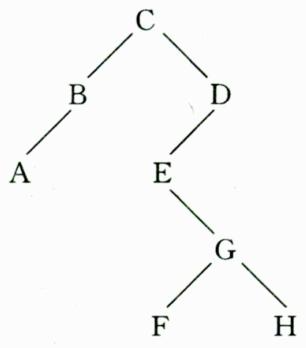
解答：根据后序序列知根结点为C，因此左子树：中序序列为AB，后序序列为AB；右子树：中序序列为EFGHD，后序序列为FHGED；依次推得该二叉树的结构图。前序序列为CBADEGFH。

例4：已知结点的前序序列为ABCDEFG，中序序列为CBEDAFG。构造出二叉树。过程见下图:

2. 二叉树的性质

• 性质1：在二叉树的第i层上最多有 $2^{i - 1}$ 个结点 $(i ≥1)$。
  证明：很简单，用归纳法。当 $i = 1$ 时， $2^{i - 1}=1$ 显然成立；现在假设第i - 1层时命题成立，即第i - 1层上最多有 $2^{i - 2}$ 个结点。由于二叉树的每个结点的度最多为2，故在第i层上的最大结点数为第i - 1层的2倍，即 $2 * 2^{i - 2}=2^{i - 1}$。
• 性质2：深度为k的二叉树至多有 $2^{k}-1$ 个结点 $(k ≥1)$。
  证明：在具有相同深度的二叉树中，仅当每一层都含有最大结点数时，其树中结点数最多。因此利用性质1可得，深度为k的二叉树的结点数至多为 $2^{0}+2^{1}+\cdots+2^{k - 1}=2^{k}-1$ ，故命题正确。

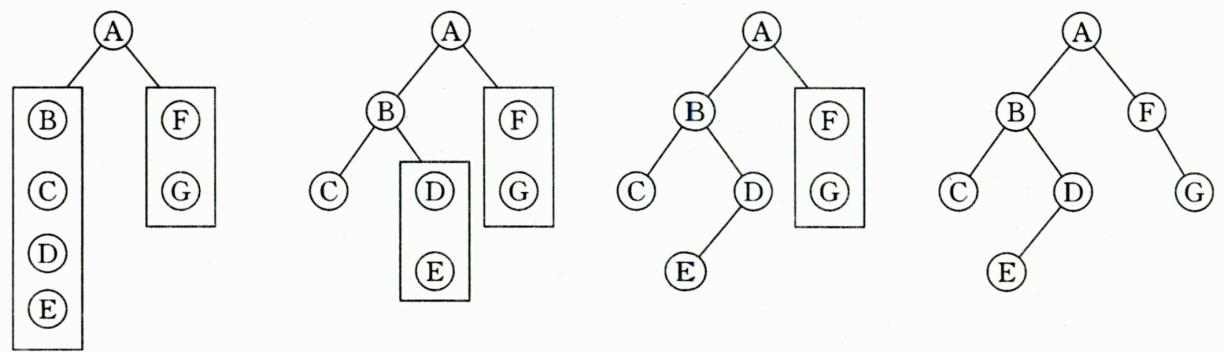
特别：一棵深度为k且有 $2^k - 1$ 个结点的二叉树称为满二叉树。这种树的特点是每层上的结点数都是最大结点数。可以对满二叉树的结点进行连续编号，约定编号从根结点起，自上而下，从左到右，由此引出完全二叉树的定义，深度为k，有n个结点的二叉树当且仅当其每一个结点都与深度为k的满二叉树中编号从1到n的结点一一对应时，称为完全二叉树。

下图B就是一个深度为4,结点数为12的完全二叉树。它有如下特征:叶结点只可能在 层次最大的两层上出现;对任一结点,若其右分支下的子孙的最大层次为m,则在其左分支 下的子孙的最大层次必为m或m+1。下图C、D不是完全二叉树,请大家思考为什么?

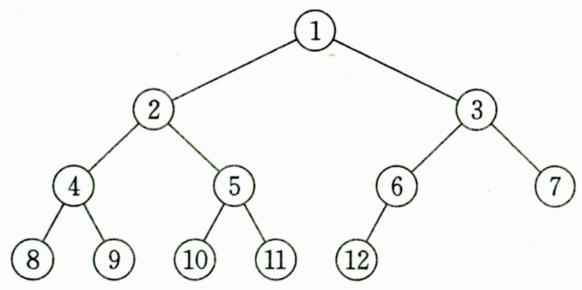
• 性质3：对任意一棵二叉树，如果其叶结点数为 $n_{0}$ ，度为2的结点数为 $n_{2}$ ，则一定满足 $n_{0}=n_{2}+1$。
  证明：因为二叉树中所有结点的度数均不大于2，所以结点总数(记为n)应等于0度结点数 $n_{0}$ 、1度结点 $n_{1}$ 和2度结点数 $n_{2}$ 之和: $n=n_{0}+n_{1}+n_{2} \cdots \cdots (式子 1)$ 另一方面，1度结点有一个孩子，2度结点有两个孩子，故二叉树中孩子结点总数是 $n_{1}+2 n_{2}$，树中只有根结点不是任何结点的孩子，故二叉树中的结点总数又可表示为 $n=n_{1}+2 n_{2}+1 \cdots \cdots( 式子 2)$ 由式子1和式子2得到: $n_{0}=n_{2}+1$

• 性质4：具有n个结点的完全二叉树的深度为 $floor (log _{2} n)+1$。
  证明：假设深度为k，根据完全二叉树的定义，前面k - 1层一定是满的，所以 $n>2^{k - 1}-1$ 。但n又要满足 $n ≤2^{k}-1$ 。所以， $2^{k - 1}-1<n ≤2^{k}-1$ 。变换一下为 $2^{k - 1} ≤n<2^{k}$ 。以2为底取对数得到: $k - 1 ≤log _{2} n<k$ 。而k是整数，所以 $k= floor (log _{2} n)+1$。

• 性质5：具有n个结点的二叉树的高度至少为 $log _{2}(n + 1)$。
  证明：根据"性质2"可知，高度为k的二叉树最多有 $2^{k}-1$ 个结点。反之，对于包含n个节点的二叉树的高度至少为 $log _{2}(n + 1)$。

• 性质6：对于一棵n个结点的完全二叉树的任一个结点(编号为i)，有以下关系:

  • 如果 $i = 1$ ，则结点i为根，无父结点；如果 $i>1$ ，则其父结点编号为 $i/2$。
  • 如果 $2 * i>n$ ，则结点i无左孩子，否则左孩子编号为 $2*i$ 。如果 $2 * i+1>n$ ，则结点i无右孩子，否则右孩子编号为 $2*i+1$。
    证明：略，我们只要验证一下即可，总结如下图。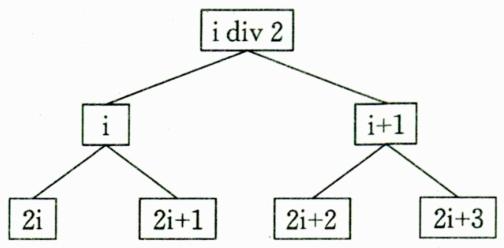 结点i和i+1在同一层上 结点i和i+1不在同一层上