第二章 程序设计基础知识

第9节 图

图（Graph）是一种复杂的非线性结构。在人工智能、工程、数学、物理、化学、生物和计算机科学等领域中，图结构有着广泛的应用。

一、图的定义

点用边连起来就叫作图，严格意义上讲，图是一种数据结构，定义为graph=(V, E) 。V是一个非空有限集合，代表顶点（结点），E代表边的集合。

二、图的相关概念

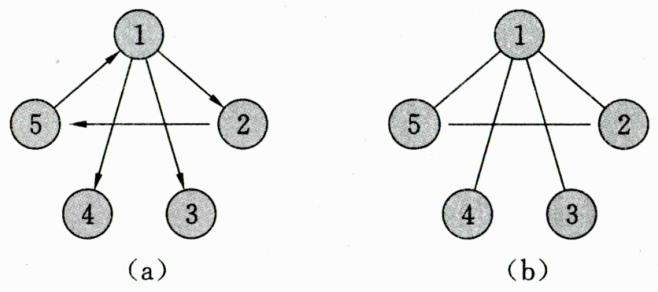
1. 有向图：图的边有方向，只能按箭头方向从一点到另一点，(a)就是一个有向图。

2. 无向图：图的边没有方向，可以双向，(b)就是一个无向图。

3. 结点的度：无向图中与结点相连的边的数目，称为结点的度。

4. 结点的入度：在有向图中，以这个结点为终点的有向边的数目。

5. 结点的出度：在有向图中，以这个结点为起点的有向边的数目。

6. 权值：边的“费用”，可以形象地理解为边的长度。

7. 连通：如果图中结点U，V之间存在一条从U通过若干条边、点到达V的通路，则称U、V是连通的。

8. 回路：起点和终点相同的路径，称为回路，或“环”。

9. 完全图：一个n阶的完全无向图含有 $n *(n - 1)/2$ 条边，一个n阶的完全有向图含有 $n *(n - 1)$ 条边。

10. 稠密图：一个边数接近完全图的图。

11. 稀疏图：一个边数远远少于完全图的图。

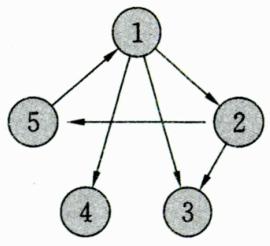
12. 强连通分量：有向图中任意两点都连通的最大子图。右图中，1-2-5构成一个强连通分量。特殊地，单个点也算一个强连通分量，所以右图有三个强连通分量：1-2-5，4，3。

三、图的存储结构

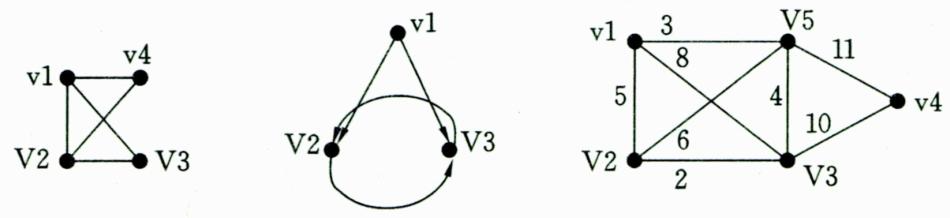
1. 二维数组邻接矩阵存储：图的邻接矩阵存储方式是用一个二维数组（称邻接矩阵）存储图中的边或弧的信息。它适用于稠密图。 定义int G[101][101]，其中G[i][j]表示从点i到点j的边的权值，定义如下：

2. 邻接表存储结构：邻接表是一种将数组与链表相结合的存储方法，其具体实现为：将图中顶点用一个一维数组存储，每个顶点Vi的所有邻接点用一个单链表来存储，链表中存放与当前结点相邻的结点在数组中的下标，适用于稀疏图。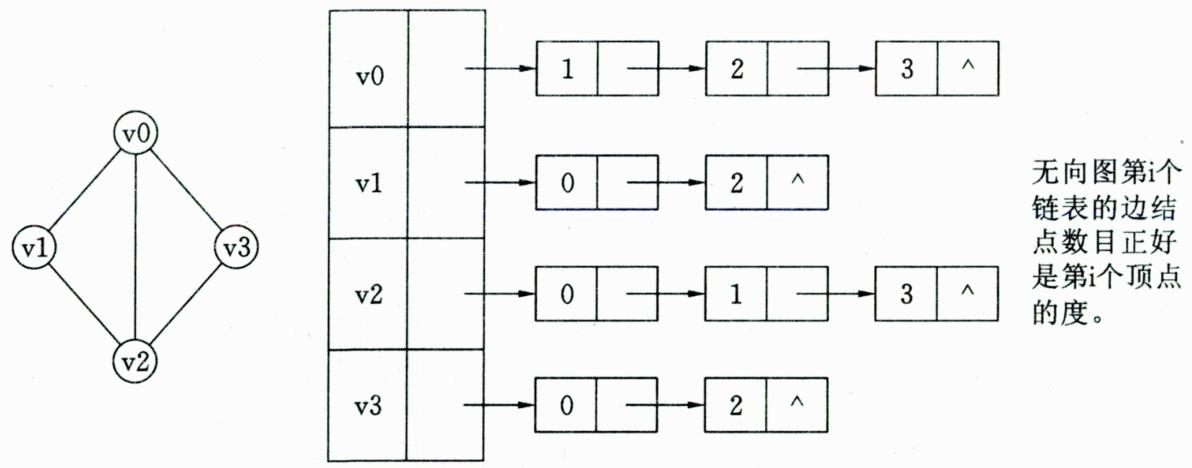

对于具有n个结点、e条边的无向图，邻接表中数组有n个顶点结点、链表有2e个边结点。

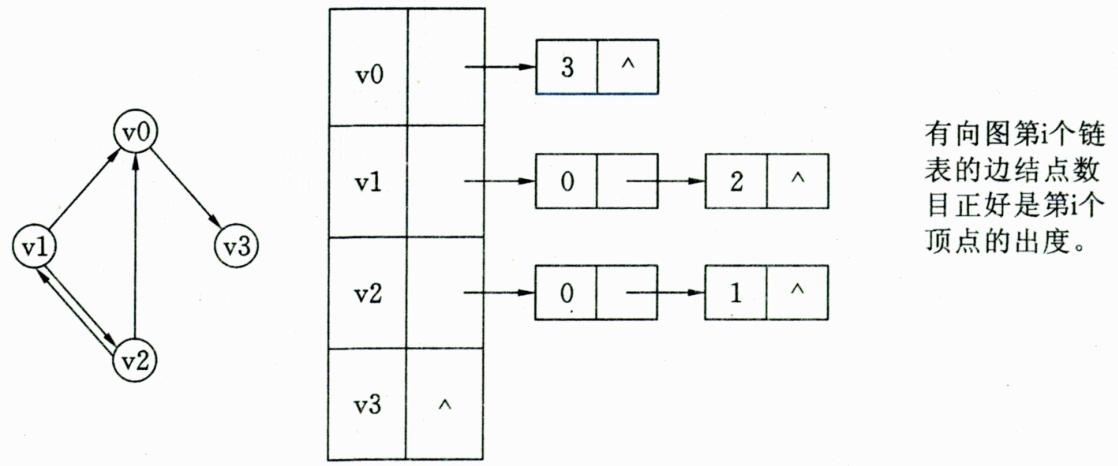
对于具有n个结点、e条边的有向图，邻接表中数组有n个顶点结点、链表有e个边结点。

四、深度优先与广度优先遍历

从图中某一顶点出发系统地访问图中所有顶点，使每个顶点恰好被访问一次，这种运算操作被称为图的遍历。为了避免重复访问某个顶点，可以设一个标志数组visited[i]，未访问时值为false，访问一次后改为true。图的遍历分为深度优先遍历和广度优先遍历两种方法，两者的时间效率都是 $O(n * n)$ 。

1. 深度优先遍历：深度优先遍历与深度搜索算法相似，从一个点A出发，将这个点标为已访问visited[i]=true，然后再访问所有与之相连且未被访问过的点。当A的所有邻接点都被访问过后，退回到A的上一个点（假设是B），再从B的另一个未被访问的邻接点出发，继续遍历。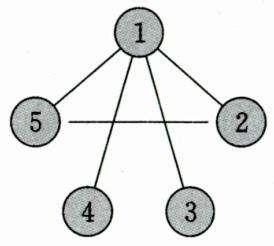

2. 广度优先遍历：广度优先遍历并不常用，从编程复杂度的角度考虑，通常采用的是深度优先遍历。

广度优先遍历和广度优先搜索相似，因此使用广度优先遍历一张图并不需要掌握新的知识，在原有的广度优先搜索的基础上，做一些小的修改，就变成广度优先遍历算法。

五、一笔画问题

如果一个图存在一笔画，则一笔画的路径叫作欧拉路，如果最后又回到起点，那这个路径叫作欧拉回路。 定义奇点是指跟这个点相连的边数目有奇数个的点。对于能够一笔画的图，有以下两个定理。 定理1：存在欧拉路的条件，图是连通的，有且只有2个奇点。 定理2：存在欧拉回路的条件，图是连通的，有0个奇点。 两个定理的正确性是显而易见的，既然每条边都要经过一次，那么对于欧拉路，除了起点和终点外，每个点如果进入了一次，一定要出去一次，显然是偶点。对于欧拉回路，每个点进入和出去次数一定都是相等的，显然没有奇点。 求欧拉路的算法很简单，使用深度优先遍历即可。 根据一笔画的两个定理，如果寻找欧拉回路，对任意一个点执行深度优先遍历；找欧拉路，则对一个奇点执行深度优先搜索，时间复杂度为O(m + n)，m为边数，n是点数。