🔍 算法基础与复杂度分析：从概念到应用
✨ 算法核心概念
算法是解决特定问题的一系列清晰、有限的指令步骤。它必须具备以下五个基本特性：
- 有穷性：算法必须在执行有限步骤后结束。
- 确定性：算法的每一步骤都必须有明确的定义，不会产生二义性。
- 可行性：算法的每一步骤都必须能够通过有限次基本操作完成。
- 输入：算法有零个或多个输入。
- 输出：算法有一个或多个输出，输出与输入有特定关系。
评价一个算法的优劣，主要标准是正确性、可读性、健壮性（对不合理输入的反应能力）以及效率。效率通常通过时间复杂度和空间复杂度来衡量，这也是竞赛考核的重点。
⏱️ 时间复杂度 (Time Complexity)
时间复杂度并不是计算程序具体的运行时间，而是算法执行基本操作次数相对于输入规模 n 的增长趋势，通常用大 O 符号表示。
- 常见时间复杂度（按效率从高到低排列）：
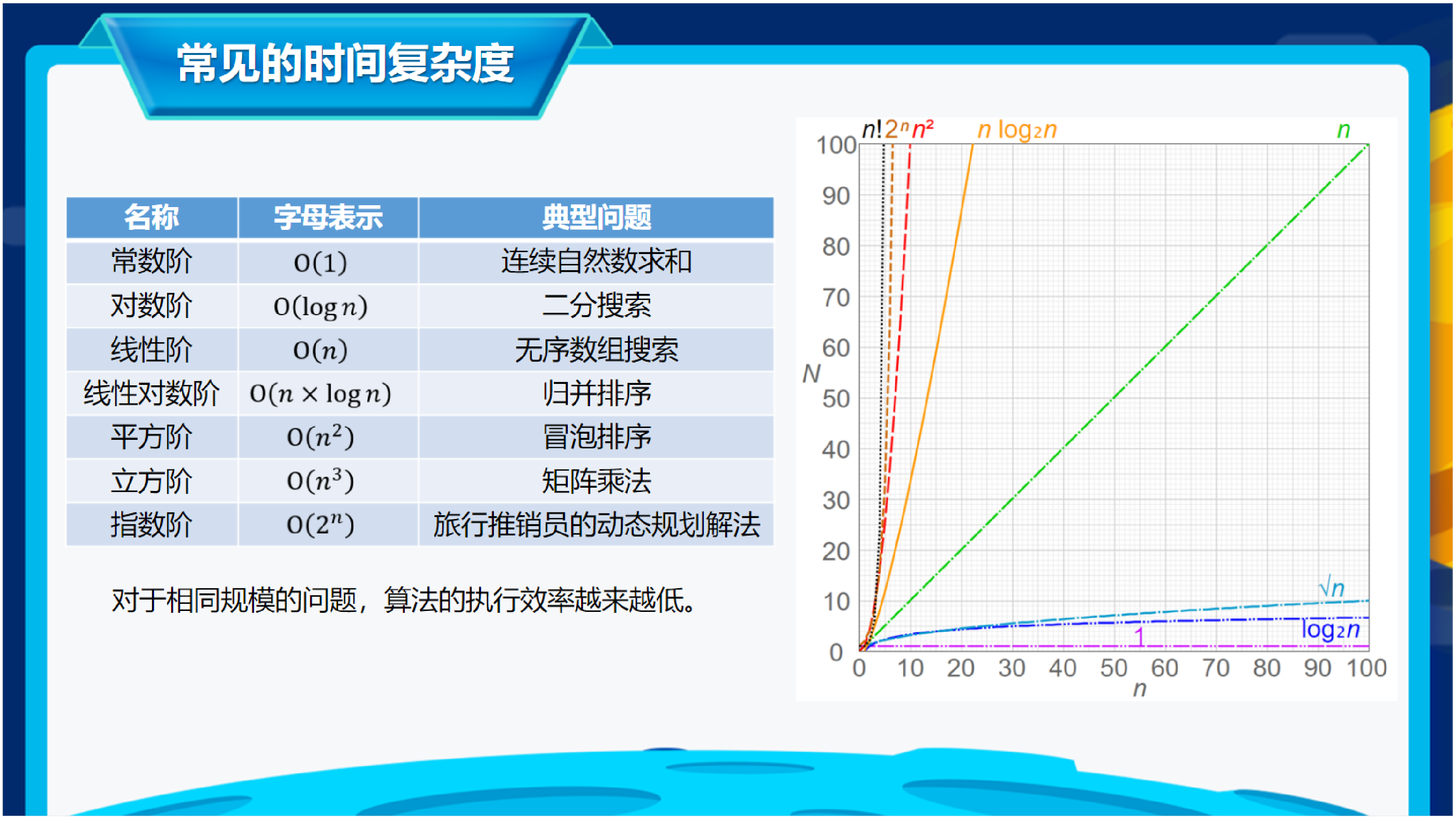
- 简化规则：计算复杂度时，我们只关注最高次项，并忽略其系数。例如，如果基本操作次数是 T(n) = 3n² + 2n + 1，那么我们记其时间复杂度为 O(n²)。
💾 空间复杂度 (Space Complexity)
空间复杂度衡量的是算法在运行过程中临时占用的存储空间大小随输入规模 n 的增长趋势。同样使用大 O 表示法。
- 算法占用的空间主要包括：
- 指令空间：存储程序代码本身。
- 数据空间：存储常量、变量、输入输出数据。
- 环境栈空间：存储函数调用所需的信息（如返回地址、形参等）。
- 在竞赛中，我们主要关注数据空间的占用。例如，定义一个大小为 n 的数组，其空间复杂度至少为 O(n)。递归算法由于其调用栈较深，通常需要更多的空间。
📊 常见算法的时间与空间复杂度
