课堂练习

1. 【NOIP2011】在使用高级语言编写程序时，一般提到的“空间复杂度”中的“空间”是指( )。
   A.程序运行时理论上所占的内存空间
   B.程序运行时理论上所占的数组空间
   C.程序运行时理论上所占的硬盘空间
   D.程序源文件理论上所占的硬盘空间
   【答案】A
   【分析】空间复杂度(Space Complexity)是对一个算法在运行过程中临时占用存储空间大小的量度，这个存储空间是指计算机内存。

2. 【NOIP2013】斐波那契数列的定义如下: $F_{1}=1$ ， $F_{2}=1$ ， $F_{n}=F_{n - 1}+F_{n - 2}(n≥3)$ 。如果用下面的函数计算斐波那契数列的第 $n$ 项，则其时间复杂度为( )。

int F(int n){
    if(n<=2)
        return 1;
    else
        return F(n - 1)+F(n - 2);
}

A. $O(1)$
B. $O(n)$
【答案】D
【分析】该函数可以理解成一棵二叉树，根节点的值等于两个子节点的和，叶子节点的值为1。函数的最终返回值为 $F_{n}$ ，因此一共有 $F_{n}$ 个叶子节点和 $F_{n}-1$ 个非叶子节点，总的时间复杂度是 $O(F_{n})$ 。

3. 【NOIP2013】 $T(n)$ 表示某个算法输入规模为 $n$ 时的运算次数。如果 $T(1)$ 为常数，且有递归式 $T(n)=2*T(n/2)+2n$ ，那么 $T(n)=( )$ 。
   A. $O(n)$
   B. $O(nlogn)$
   C. $O(n^{2})$ D. $O(n^{2}logn)$ 【答案】B
   【分析】题中的递归式，相当于归并排序的复杂度，每次分治成两个子问题，合并子问题的代价为 $n$ ，我们可以想象成共有 $logn$ 层，每次代价总共需要 $O(n)$ 。因此总的时间复杂度为 $O(nlogn)$ 。

4. 【NOIP2015】设某算法的计算时间表示为递推关系式 $T(n)=T(n - 1)+n$ ($n$ 为正整数)及 $T(0)=1$ ，则该算法的时间复杂度为( )。
   A. $O(logn)$
   B. $O(nlogm)$
   $C. O(n)$ $D. O(n^{2})$ 【答案】D
   【分析】本题考查复杂度的计算方法。 $T(n)=T(n - 1)+n=T(n - 2)+(n - 1)+n$=...=$T(0)+1+2+\cdots+n=1+\frac{(n + 1) * n}{2}$ ，所以是 $O(n^{2})$ 。

5. 【NOIP2016】假设某算法的计算时间表示为递推关系式 $T(n)=2 T\left(\frac{n}{4}\right)+\sqrt{n}$ $T(1)=1$ 则算法的时间复杂度为( )。
   A. $O(n)$
   $B. O(\sqrt{n})$ $C. O(\sqrt{n} log n)$ $D. O(n^{2})$ 【答案】C
   【分析】可以根据递推关系式一路推导得出结果:

6. 【NOIP2017】若某算法的计算时间表示为递推关系式: $T(N)=2 T( N / 2)+N log N$ $T(1)=1$ 则该算法的时间复杂度为( )。
   A. $O(N)$
   $B. O(N log N)$ $C. O(N log^{2} N)$ $D. O(N^{2})$ 【答案】C
   【分析】考查主定理。可以根据递推关系式一路推导得出结果: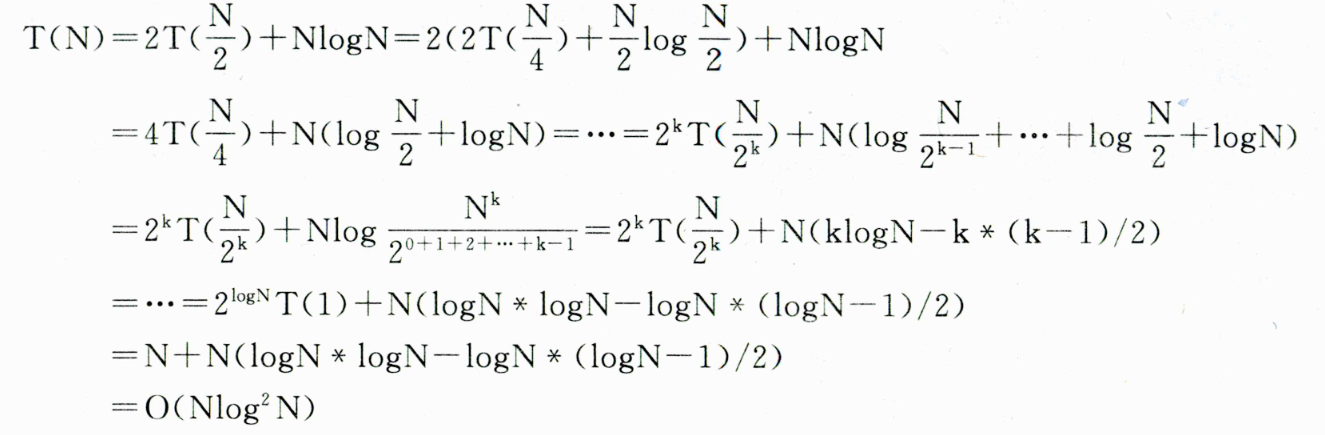

7. 【NOIP2012】如果对于所有规模为 $n$ 的输入，一个算法均恰好进行( )次运算，我们可以说该算法的时间复杂度为 $O(2^{n})$ 。
   $A. 2^{n + 1}$ B. $3^{n}$ $C. n * 2^{n}$ $D. 2^{2 n}$ 【答案】A
   【分析】计算机科学中，算法的时间复杂度是一个函数，它定量描述了该算法的运行时间。时间复杂度常用大 $O$ 符号表述，忽略这个函数的低阶项和首项系数， $2^{n + 1}=2 * 2^{n}$ 。