课堂练3

1. 【NOIP2016】周末小明和爸爸妈妈三个人一起想动手做三道菜。小明负责洗菜、爸爸负责切菜、妈妈负责炒菜。假设做每道菜的顺序都是：先洗菜10分钟，然后切菜10分钟，最后炒菜10分钟。那么做一道菜需要30分钟。注意：两道不同菜的相同步骤不可以同时进行。例如第一道菜和第二道的菜不能同时洗，也不能同时切，那么做完三道菜的最短时间需要( )分钟。
   A. 90
   B. 60
   C. 50
   D. 40
   【答案】C
   【分析】本题考查基本常识，三个人分别负责洗菜切菜炒菜，每个人完成自己的工序之后交给下一个人，那么第一道菜做完需要30分钟，但后面每10分钟都能完成一道菜，总共需要50分钟。本题的目的在于体现计算机CPU中流水线优化的意义。
2. 【NOIP2017】2017年10月1日是星期日，1999年10月1日是( )。
   A. 星期三
   B. 星期日
   C. 星期五
   D. 星期二
   【答案】C
   【分析】考查闰年与同余的相关知识。直接计算两个日期之间相差多少天即可，平年有365天，$365\%7 = 1$ ，如果2017（平年）年10月1日是星期日，那么2016年10月1日是星期六，所以得出第一个结论：两个相差一个平年的日期的星期相差1；闰年有366天，$366\%7 = 2$ ，如果2016年（闰年）10月1日是星期六，那么2015年10月1日是星期四，所以得出第二个结论：两个相差一个闰年的日期的星期相差2；1999 - 2017年相差18年，其中有5个闰年（2000，2004，2008，2012，2016），所以相差的天数为 $(0 - 18 - 5)\%7 = -2$ ，即把星期天往前推2天，答案是星期五。
3. 【NOIP2018】下面的故事与( )算法有着异曲同工之妙。 从前有座山，山里有座庙，庙里有个老和尚在给小和尚讲故事；从前有座山，山里有座庙，庙里有个老和尚在给小和尚讲故事；从前有座山，山里有座庙，庙里有个老和尚给小和尚讲故事……
   A. 枚举
   B. 递归
   C. 贪心
   D. 分治
   【答案】B
   【分析】考察算法基础知识。显然“从前有座山……”这个故事描述的是递归算法。和尚讲的故事里继续套用和尚讲故事，正如函数不断调用本身，形成递归。
4. 【NOIP2011】( )是一种选优搜索法，按选优条件向前搜索，以达到目标。当探索到某一步时，发现原先选择并不优或达不到目标，就退回一步重新选择。
   A. 回溯法
   B. 枚举法
   C. 动态规划
   D. 贪心法
   【答案】A
   【分析】搜索与回溯：因为是选优，所以排除枚举法，又因为会退回一步重新选择，而动态规划和贪心都是不会退的，所以是回溯法。
5. 【NOIP2013】将(2，6，10，17)分别存储到某个地址区间为0 - 10的哈希表中，如果哈希函数 $h(x) = ( )$ ，将不会产生冲突，其中a mod b表示a除以b的余数。
   A. $x\ mod\ 11$
   B. $x^{2}\ mod\ 11$
   C. $2x\ mod\ 11$
   D. $[\sqrt{x}]\ mod\ 11$ ，其中 $[x]$ 表示 $\sqrt{x}$ 下取整
   【答案】D
   【分析】哈希查找算法，将(2，6，10，17)代入四个选项，当我们选取D做哈希函数时，(2，6，10，17)散列后的值分别为(1，2，3，4)，不会产生冲突。A、B、C选项，6和17都产生冲突。
6. 【NOIP2012】( )就是把一个复杂的问题分成两个或者更多的相同或相似的子问题，再把子问题分成更小的子问题……直到最后的子问题可以简单的直接求解。而原问题的解就是子问题解的并。
   A. 动态规划
   B. 贪心
   C. 分治
   D. 搜索
   【答案】C
   【分析】题目大意就是分治法的定义。
7. 【NOIP2016】给定含有n个不同数的数组 $L = <x1,x2, \cdots,xn>$ 。如果L中存在 $xi (1 < i < n)$ 使得 $x1 < x2 < \cdots < xi - 1 < xi > xi + 1 > \cdots > xn$ ，则称L是单峰的，并称xi是L的“峰顶”。现在已知L是单峰的，请把a - c三行代码补全到算法中使得算法正确找到L的峰顶。

Search(1,n) 
// a.Search(k+1,n) 
// b.Search(1,k-1) 
// c.return L[k]
1.k = [n/2」
2.if L[k] > L[k - 1] and L[k] > L[k + 1]
3.then
4.else if L[k] > L[k - 1] and L[k] < L[k + 1]
5.then
6.else

正确的填空顺序是( )。
A. c，a，b
B. c，b，a
C. a，b，c
D. b，a，c
【答案】A
【分析】考查对二分查找的理解。 如果第k个数大于第k - 1个数和第k + 1个数，那么k就是峰顶； 如果第k个数大于第k - 1个数，但小于第k + 1个数，那么峰顶在k的右侧，需要在k + 1到n的范围内去寻找峰顶；否则，应该去1到k - 1范围内去寻找峰顶。 8. 【NOIP2017】在 $n(n≥3)$ 枚硬币中有一枚质量不合格的硬币（质量过轻或质量过重），如果只有一架天平可以用来称重且称重的硬币数没有限制，下面是找出这枚不合格的硬币的算法。请把a - c三行代码补全到算法中。

// a. A ← X ∪ Y
// b. A ← Z
// C. n ←|A|
算法Coin(A,n)
(1) k ← [n / 3」
(2)将A中硬币分成x，Y，Z三个集合，使得|X| = |Y| = k，|Z| = n - 2k
(3)if W(X)≠W(Y) //W(X)，W(Y)分别为x或Y的重量
(4)then
(5)else
(6)
(7)if n > 2 then go to1
(8)if n = 2 then任取A中1枚硬币与拿走硬币比较，若不等，则它不合格；若相等，则A中剩下的硬币不合格.
(9)if n = 1 thenA中硬币不合格

正确的填空顺序是( )。
A. b，c，a
B. c，b，a
C. c，a，b
D. a，b，c
【答案】D
【分析】分治：首先要理解这几个符号，a操作是将X和Y的并集赋值给A，b操作是将Z赋值给A，操作是将A集合的大小赋值给n。 那么这里其实就是一个三分的操作，第3行判断X，Y质量是否相等，如果不相等，显然不合格的硬币出现在X或Y中，那么这里要做的操作就是继续搜索X和Y的并集，所以这里填a操作。 接下来第5行，若X，Y质量相等，则不合格的硬币在Z中，所以这里填b操作。 第6行将新集合的大小更新到n，选择c操作。 9. 【NOIP2011】应用快速排序的分治思想，可以实现一个求第K大数的程序。假定不考虑极端的最坏情况，理论上可以实现的最低的算法时间复杂度为( )。
A. $O(n^{2})$
B. $O(nlogn)$
C. $O(n)$
D. $O(1)$
【答案】C
【分析】分治：应用快排的思想，随机选一个轴数k，把数列分为左右两端，一边都小于k，一边都大于等于k，然后要么在左边要么在右边。极端最好的情况，随机选的轴数k，就是需要的答案，比较的次数是 $n - 1$ 次；极端最坏的情况是这样的，随机选的轴数k是序列中的极值，不能把数列分开，每次问题的规模只能减少1；平均的情况是，每次查找范围期望缩小一半。所以复杂度就是 $n+\frac{n}{2}+\frac{n}{4}+\frac{n}{8}+\cdots<2n = O(n)$ 。综上所述，这题答案应该选C。 10. 【NOIP2014】设有100个数据元素，采用折半搜索时，最大比较次数为( )。
A. 6
B. 7
C. 8
D. 10
【答案】B
【分析】分治算法，在 $2^{n}-1$ 个元素中采用折半搜索，最大比较次数为n次。而 $2^{6}-1 = 63 < 100 < 127 = 2^{7}-1$ 。 11. 【NOIP2009】有一个由4000个整数构成的顺序表，假定表中的元素已经按升序排列，采用二分查找定位一个元素。则最多需要( )比较就能确定是否存在所查找的元素。
A. 11次
B. 12次
C. 13次
D. 14次
【答案】B
【分析】分治：在二分查找的时候，可以每次去掉总数的一半，最后剩下1个的时候，就说明找到了，每次剩下的总数变化过程为：4000 -> 2000 -> 1000 -> 500 -> 250 -> 125 -> 63 -> 32 -> 16 -> 8 -> 4 -> 2 -> 1；则只需要12次就可以定位到所需元素。我们还可以发现， $2^{11}-1 = 2047$ ， $2^{12}-1 = 4095$ ，排序二叉树高度也为12。 12. 【NOIP2008】对有序数组(5，13，19，21，37，56，64，75，88，92，100)进行二分查找，成功查找元素19的查找长度（比较次数）是( )。
A. 1
B. 2
C. 3
D. 4
【答案】B
【分析】分治算法，需要了解二分查找，也叫折半查找。第一次 $l = 1$ ， $r = 11$ ， $mid = 6$ ， $a[mid] = 56$ ，第二次 $l = 1$ ， $r = 5$ ， $mid = 3$ ， $a[mid] = 19$ 。 13. 【NOIP2008】对有序数组(5，13，19，21，37，56，64，71，88，92，100)进行二分查找，等概率的情况下查找成功的平均查找长度（平均比较次数）是( )。
A. $35/11$
B. $34/11$
C. $33/11$
D. $32/11$
E. $34/10$
【答案】C
【分析】分治算法，根据二分查找的特点，可以构造二叉树（见下图所示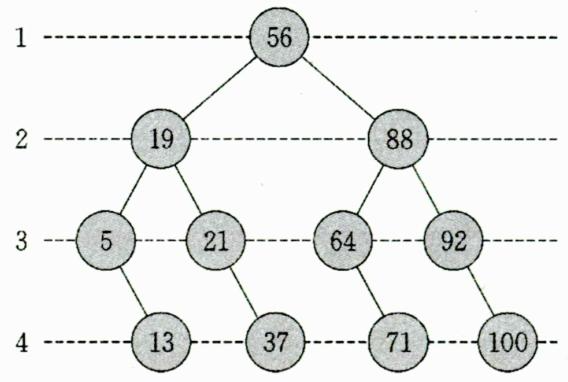）： 56需要查找1次；19和88需要查找2次；5、21、64、92需要查找3次，13、37、71、100需要查找4次，平均查找长度（ASL）=查找次数和/总个数= $(1×1 + 2×2 + 3×4 + 4×4)÷11 = 33÷11 = 3$ 。 14. 【NOIP2015】在数据压缩编码的应用中，哈夫曼（Huffman）算法是一种采用了( )思想的算法。
A. 贪心
B. 分治
C. 递推
D. 回溯
【答案】A
【分析】哈夫曼算法用了贪心思想。 15. 【NOIP2008】将数组(8，23，4，16，77，-5，53，100)中的元素按从大到小的顺序排列，每次可以交换任意两个元素，最少需要交换( )次。
A. 4
B. 5
C. 6
D. 7
【答案】B
【分析】贪心：先将数据从大到小排好序，即(100，77，53，23，16，8，4，-5)，与原序列(8，23，4，16，77，-5，53，100)进行比较。通过1次交换，最好的情况是2个数归位，可以发现4、53形成一个轮换序列，用1次交换，可以使这两个数归位；然后，考虑通过2次交换，最好的情况是有3个数归位，我们发现其中100、8、-5形成一个轮换序列，需要2次交换，其中77、23、16形成一个轮换序列，需要2次交换，至此序列已经有序了，总计5次交换。 16. 【NOIP2018】给定一个含N个不相同数字的数组，在最坏情况下，找出其中最大或最小的数，至少需要N-1次比较操作。则最坏情况下，在该数组中同时找最大与最小的数至少需要( )次比较操作。（$\lceil\rceil$表示向上取整，$\lfloor\rfloor$表示向下取整）
A. $\lceil3N/2\rceil-2$
B. $\lfloor3N/2\rfloor-2$
C. 2N-2
D. 2N-4
【答案】A
【分析】贪心：数组大小为N，若N为偶数，则需要 $\frac{3×(N-2)}{2}+1 = \frac{3N}{2}-2$ 次比较；若N为奇数，则需要 $\frac{3(N-1)}{2}$ 次比较，偶数先比前两个数、作为最大值和最小值的初始值，需要一次比较次数。奇数将第一个元素作为最大值和最小值的初始值。再以两个数为一组，首先比较这两个数的大小，然后分别与当前最小值和最大值比较，两个公式可以合并成 $\lceil\frac{3N}{2}\rceil-2$ 。问题规模缩减的策略类似过河问题，策略一：一次性减少2个规模，需要3次比较。策略二：一次性减少1个规模，需要2次比较，当用策略二减少2个规模时，需要4次比较，因此贪心选择策略一。 17. 【NOIP2017】有正实数构成的数字三角形排列形式。第一行的数为a，第二行的数从左到右依次为 $a_{21},a_{22},\cdots$ ，第n行的数为 $a_{n1},a_{n2},\cdots,a_{nn}$ 。从 $a_{11}$ 开始，每一行的数 $a_{ij}$ 只有两条边可以分别通向下一行的两个数 $a_{(i+1)j}$ 和 $a_{(i+1)(j+1)}$ 。用动态规划算法找出一条从 $a_{11}$ 向下通到 $a_{n1},a_{n2},\cdots,a_{nn}$ 中某个数的路径，使得该路径上的数之和达到最大。令 $C[i,j]$ 是从 $a_{11}$ 到 $a_{ij}$ 的路径上的数的最大和，并且 $C[i,0]=C[0,j]=0$ ，则 $C[i,j]=( )$ 。
A. $\max\{C[i-1,j-1],C[i-1,j]\}+a_{ij}$
B. $C[i-1,j-1]+C[i-1,j]$
C. $\max\{C[i-1,j-1],C[i-1,j]\}+1$
D. $\max\{C[i,j-1],C[i-1,j]\}+a_{ij}$
【答案】A
【分析】经典dp，每个位置 $C[i,j]$ 可以由 $C[i-1][j-1]$ ，$C[i-1][j]$ 两个状态更新，那么要求路径和最大，则取这两个位置的较大值，加上当前这个结点上的数字 $a_{ij}$ 。

不定项选择题

1. 【NOIP2009】散列表的地址区间为0-10，散列函数为 $H(K)=K\%11$ 。采用开地址法的线性探查法处理冲突，并将关键字序列26，25，72，38，8，18，59存储到散列表中，这些元素存入散列表的顺序并不确定。假定之前散列表为空，则元素59存放在散列表中的可能地址有( )。
   A. 5
   B. 7
   C. 9
   D. 10
   【答案】ABC
   【分析】搜索计算各个的散列值，分别为4、3、6、5、8、7、4。5有可能为26、59，7有可能为26、38、72、59，9有可能为26、38、72、18、8、59。
2. 【NOIP2012】从顶点 $A_0$ 出发，对有向图( )进行广度优先搜索（BFS）时，一种可能的遍历顺序是 $A_0,A_1,A_2,A_3,A_4$ 。
   【答案】AD
   【分析】搜索，广度优先搜索相对于是树上的层次遍历，要按照队列的进队出队完成操作，B中的 $A_2$ 节点不能在第3位访问到；C中 $A_3$ 是最后一个访问到；所以B和C都不符合要求。
3. 【NOIP2013】以 $A_0$ 作为起点，对下面的无向图进行深度优先遍历时（遍历的顺序与顶点字母的下标无关），最后一个遍历到的顶点可能是( )。
   A. $A_1$
   B. $A_2$
   C. $A_3$
   D. $A_4$
   【答案】CD
   【分析】搜索，从题中右图 $A_0$ 出发深度优先遍历，有3种可能的路径：$(A_0,A_1,A_2,A_3,A_4)$ ，$(A_0,A_1,A_4,A_2,A_3)$ ，$(A_0,A_3,A_2,A_1,A_4)$ ，因此 $A_1$ 、$A_2$ 不可能是最后遍历到的顶点。
4. 【NOIP2011】现有一段文言文，要通过二进制哈夫曼编码进行压缩。简单起见，假设这段文言文只由4个汉字“之”“乎”“者”“也”组成，它们出现的次数分别为700、600、300、400。那么，“也”字的编码长度可能是( )。
   A. 1
   B. 2
   C. 3
   D. 4
   【答案】BC
   【分析】贪心，哈夫曼编码采取贪心思想，它实际上是构建了一棵二叉树，每次取出权重最小的两个点合并成新的点，新点权重为原来权重的和。最后这个点编码长度就是所在深度-1。这题最后的二叉树形态可能有两种： 第一种：先合并300和400得到700，再合并600和700得到1300，再合并700和1300得到2000，“也”字（400）在第二层，编码长度为2； 第二种：先合并300和400得到700，再合并700和600得到1300，再合并700和1300得到2000，“也”字（400）在第二层，编码长度为2；或者先合并300和400得到700，合并700和700得到1400，合并600和1400得到2000，“也”字（400）在第二层，编码长度为2；或者其他可能的合并顺序中，“也”字可能在第三层，编码长度为3。